 |
1. TABLEAUX |
Dans ce chapitre, nous allons présenter deux méthodes pour trier
les éléments d'un tableau. Nous ne présenterons pas les algorithmes les plus
efficaces. Nous avons choisi de présenter tout d'abord la méthode de tri dite
"par sélection". Il s'agit d'une méthode qui n'est pas très rapide.
Ensuite, nous présenterons la méthode dite "par fusion" qui est beaucoup
plus efficace. Dans ce chapitre, nous utiliserons la fonction PLUS_PETIT(a,b) pour
trier. Cette fonction renvoie VRAI si l'élément a est plus
petit que l'élément b.
Cette méthode est très simple. Supposons que l'on veuille trier
les n éléments du tableau t. On commence par parcourir le
tableau pour trouver la plus petite valeur. On la place à l'indice 0. Ensuite,
on recommence à parcourir le tableau à partir de l'indice 1 pour trouver
la plus petite valeur que l'on stocke à l'indice 1. Et ainsi de suite pour
l'indice 2, 3 jusqu'à n - 2. La figure suivante
montre comment l'algorithme fonctionne sur un tableau de 8 éléments.
Seulement quelques étapes sont représentées.

La fonction se déroule de la manière suivante. Le tableau est
parcouru du premier élément (indice 0) à l'avant dernier (indice
n - 2). On note i l'indice de l'élément visité
à une itération donnée. On compare l'élément i avec
chaque élément j qui suit dans le tableau, c'est-à-dire de
l'indice i + 1 jusqu'à l'indice n - 1. Si l'élément
d'indice j est plus petit que l'élément d'indice i alors on
permute i et j dans le tableau. Voici le détail de la fonction de
tri.
fonction trierSelection(ELEMENT * t, ENTIER n):
i  0; 0;
tant que (i < n - 1) faire
j  i + 1; i + 1;
tant que (j < n) faire
si (PLUS_PETIT(t[j],t[i])) alors
tmp  t[j]; t[j];
t[j]  t[i]; t[i];
t[i]  tmp; tmp;
fin si;
j  j + 1; j + 1;
fin tant que;
i  i + 1; i + 1;
fin tant que;
fin fonction;
L'idée de cette méthode est la suivante. Pour trier un tableau
t de n éléments, on le scinde en deux tableaux de
même taille (à un élément près). On les note t1 de
taille n1 et t2 de taille n - n1. Ces deux tableaux sont
ensuite triés (appel récursif) et enfin fusionnés de manière à
reformer le tableau t trié. La figure suivante reprend l'exemple du tri par
sélection et montre comment le tri par fusion fonctionne au travers d'étapes
numérotées de 1 à 21.
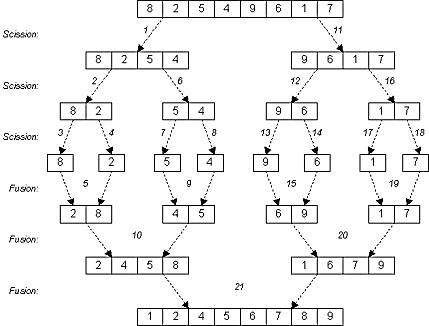
Pour réaliser ce tri, on a besoin de plusieurs fonctions dont voici la
liste.
scinder(ELEMENT * t, ENTIER n, ELEMENT * t1,
ENTIER n1, ELEMENT * t2)
Copie les n1 premiers éléments du tableau t dans un tableau
t1 et le reste dans un tableau t2.
ENTIER  concatener(ELEMENT * t1, ENTIER n1, ELEMENT * t2, concatener(ELEMENT * t1, ENTIER n1, ELEMENT * t2,
ENTIER
n2, ENTIER i2)
Copie le tableau t2 de taille n2 à la fin du tableau
t1 de taille initiale n1. La copie débute à l'indice
i2 dans t2. Après la copie, la nouvelle taille de t1
est retournée par la fonction.
fusionner(ELEMENT * t, ELEMENT * t1, ENTIER n1,
ELEMENT * t2, ENTIER n2)
Recopie les éléments des tableaux t1 et t2 dans le tableau
t de façon à ce qu'ils soient triés. Les éléments
de t1 et de t2 sont supposés triés.
trierFusion(ELEMENT * t, ENTIER n)
Trie les n éléments du tableau t par la méthode de
tri par fusion.
La fonction scinder copie les n1 premiers
éléments du tableau t dans t1 et le reste dans
t2.
fonction scinder( |
ELEMENT * t, ENTIER n, ELEMENT * t1,
ENTIER n1, ELEMENT * t2): |
i  0; 0;
j  0; 0;
tant que (i < n1) faire
t1[i]  t[i]; t[i];
i  i + 1: i + 1:
fin tant que;
tant que (i < n) faire
t2[j]  t[i]; t[i];
j  j + 1; j + 1;
i  i + 1; i + 1;
fin tant que;
fin fonction;
Cette fonction copie le tableau t2 à la fin du tableau
t1 de taille initiale n1. On suppose que t1 a la
capacité suffisante pour recevoir tous les éléments de t2. Le
tableau t2 est parcouru, en commençant à partir de l'indice
i2. Chaque case de t2 visitée est copiée à l'indice
n1 qui est augmenté d'une unité. A la fin de l'exécution,
n1 est retourné puisqu'il exprime la nouvelle taille de t1.
fonction ENTIER  concatener(
concatener( |
ELEMENT * t1, ENTIER n1,
ELEMENT * t2, ENTIER n2,
ENTIER i2): |
i  0; 0;
tant que (i < n2) faire
t1[n1]  t2[i2 + i]; t2[i2 + i];
n1  n1 + 1; n1 + 1;
i  i + 1; i + 1;
fin tant que;
rendre n1;
fin fonction;
Cette fonction fusionne les deux tableaux t1 de taille
n1 et t2 de taille n2 supposés triés dans le
tableau t. La fusion se fait de façon à ce que t soit
trié. Pour cela, on parcours t1 et t2 parallèlement. Quand
l'élément visité dans t1 est plus petit que celui visité
dans t2, on copie l'élément de t1 dans t et on
passe à l'élément suivant de t1, sinon on copie celui de
t2 et on avance dans t2. On progresse comme cela jusqu'à ce que
l'un des deux tableaux ait été complètement visité. Dans ce cas, on
copie la partie non visitée de l'autre tableau directement dans t.
fonction fusionner( |
ELEMENT * t, ELEMENT * t1, ENTIER n1,
ELEMENT * t2, ENTIER n2): |
i1  0; 0;
i2  0; 0;
i  0; 0;
tant que (i1 < n1 et i2 < n2) faire
si (PLUS_PETIT(t1[i1],t2[i2])) alors
t[i]  t1[i1]; t1[i1];
i1  i1 + 1; i1 + 1;
sinon
t[i]  t2[i2]; t2[i2];
i2  i2 + 1; i2 + 1;
fin si;
i  i + 1; i + 1;
fin tant que;
i  concatener(t,i,t1,n1 - i1,i1); concatener(t,i,t1,n1 - i1,i1);
concatener(t,i,t2,n2 - i2,i2);
fin fonction;
| |
| Trier un tableau par fusion |
| |
Cette fonction effectue le tri du tableau t de n
éléments. Elle alloue d'abord la mémoire nécessaire pour
t1 et t2. Ensuite, elle copie chaque moitié de t dans
t1 et t2. Ensuite, par appel récursif, elle trie les tableaux
t1 et t2. Enfin, elle fusionne ces deux tableaux dans t et
libère la mémoire occupée par t1 et t2. On utilise
la fonction ENT qui retourne la partie entière d'un nombre.
fonction trierFusion(ELEMENT * t, ENTIER n):
si (n > 1) alors
n1  ENT(n / 2); ENT(n / 2);
t1  ALLOUER(ELEMENT,n1); ALLOUER(ELEMENT,n1);
t2  ALLOUER(ELEMENT,n - n1); ALLOUER(ELEMENT,n - n1);
si (t1
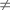 nil et
t2 nil et
t2 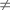 nil) alors
nil) alors
scinder(t,n,t1,n1,t2);
trierFusion(t1,n1);
trierFusion(t2,n - n1);
fusionner(t,t1,n1,t2,n - n1);
LIBERER(t1);
LIBERER(t2);
sinon
/* Erreur: Pas assez de mémoire. */
si (t1
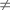 nil)
LIBERER(t1); nil)
LIBERER(t1);
si (t2
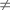 nil)
LIBERER(t2); nil)
LIBERER(t2);
fin si;
fin si;
fin fonction;
Dans ce chapitre, nous avons vu deux méthodes pour trier les
éléments d'un tableau. La méthode par sélection est très simple
à mettre en oeuvre et nécessite peu de mémoire. Par contre, elle est
très lente. A l'opposé, la méthode par fusion est un peu plus
compliquée à écrire et nécessite beaucoup plus de mémoire. En
contrepartie, elle est plus rapide.
En effet, la méthode par sélection effectue un nombre
d'opérations de l'ordre de n2 opérations pour
un tableau de n éléments. La méthode par fusion effectue quant
à elle n log(n) opérations pour un tableau de même taille. Pour
simplifier, log(n) peut être vu comme le nombre de fois que l'on peut diviser le
nombre n par 2 avant d'arriver à 1. Par exemple,
245 / 2 = 122, 122 / 2 = 61, 61 /
2 = 30, 30 / 2 = 15, 15 / 2 = 7,
7 / 2 = 3, 3 / 2 = 1. Donc, on considérera que
log(245) vaut 7.
| |
| |
| Copyright (c) 1999-2016 - Bruno Bachelet - bruno@nawouak.net -
http://www.nawouak.net |
| La permission est accordée de copier, distribuer et/ou modifier ce document
sous les termes de la licence GNU Free Documentation License, Version 1.1 ou toute
version ultérieure publiée par la fondation Free Software Foundation. Voir
cette licence pour plus de détails (http://www.gnu.org). |
|
|
|

 0;
0; i + 1;
i + 1; t[j];
t[j]; t[i];
t[i];
 tmp;
tmp;
 j + 1;
j + 1; i + 1;
i + 1; concatener(ELEMENT * t1, ENTIER n1, ELEMENT * t2,
concatener(ELEMENT * t1, ENTIER n1, ELEMENT * t2,0;
0;
t[i];
i + 1:
t[i];
j + 1;
i + 1;
concatener(
0;
t2[i2 + i];
n1 + 1;
i + 1;
0;
0;
0;
t1[i1];
i1 + 1;
t2[i2];
i2 + 1;
i + 1;
concatener(t,i,t1,n1 - i1,i1);
 ENT(n / 2);
ENT(n / 2); ALLOUER(ELEMENT,n1);
ALLOUER(ELEMENT,n1); ALLOUER(ELEMENT,n - n1);
ALLOUER(ELEMENT,n - n1);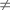 nil et
t2
nil et
t2 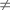 nil) alors
nil) alors 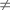 nil)
LIBERER(t1);
nil)
LIBERER(t1); nil)
LIBERER(t2);
nil)
LIBERER(t2);
