 |
4. EFFICACITE DES ALGORITHMES, COMPLEXITE DES PROBLEMES |
| INTRODUCTION |
Considérons le jeu d'échecs. On sait qu'il existe une procédure finie qui permet de déterminer la meilleure stratégie à partir d'une situation donnée. Cependant, jusqu'à présent, on ne connaît pas d'autre méthode que l'exploration de tous les coups possibles. En résumé, on sait qu'en un temps fini, on peut apporter la solution au problème. Cependant, sur le plan pratique on s'aperçoit immédiatement que l'énumération exhaustive prendrait trop de temps. La première notion qui apparaît donc est celle d'algorithme efficace. Pour un problème donné, on cherche à avoir un algorithme dit efficace, c'est-à-dire que le temps nécessaire à son exécution ne soit pas trop important. Ensuite, intervient la notion de problème facile ou difficile. Un problème sera dit facile si on peut le résoudre facilement, autrement dit s'il ne faut pas trop de temps pour trouver la solution. Ainsi, s'il existe un algorithme efficace pour un problème donné, alors ce dernier est dit facile. Mais comment caractériser les problèmes difficiles. Un problème pour lequel on ne connaît pas d'algorithme efficace, est-il difficile ou facile ? Ce n'est pas parce que l'on ne connaît pas d'algorithme efficace qu'il n'est pas facile et qu'un jour on ne trouvera pas un moyen de le résoudre. A l'inverse, il peut exister des problèmes intrinsèquement compliqués, pour lesquels on ne pourra jamais trouver d'algorithme efficace.
De nombreuses personnes se sont penchées sur ces problèmes et ont développé une théorie dite de la complexité. Nous ne verrons pas ici en détail les fondements de cette théorie mais tenterons plutôt d'acquérir une vision globale de cette problématique. Dans un premier temps, on va voir comment l'efficacité d'un algorithme est mesurée avant de définir plus précisément ce qu'est un algorithme efficace. Ensuite, On discutera de la classification des problèmes selon leur difficulté à être résolus.
| COMPLEXITE D'UN ALGORITHME |
On désigne par complexité d'un algorithme le nombre d'opérations nécessaires à celui-ci pour s'exécuter. Bien évidemment, ce nombre peut varier en fonction de ce que l'on appelle les données d'entrées, c'est-à-dire les paramètres que l'on donne à l'algorithme. Par exemple, un algorithme de tri d'éléments dans un tableau ne s'exécutera pas avec le même nombre d'opérations s'il y a 10 éléments ou s'il y en a 100. Ainsi, on cherchera à estimer la complexité d'un algorithme en fonction de la taille des données entrées. Par exemple, dans le cas du tableau, on exprimera la complexité en fonction de la taille du tableau. Pour une matrice, ce serait en fonction de sa largeur et de sa hauteur. De plus, la nature même des données pour une même taille peut ne pas aboutir au même nombre d'opérations à l'exécution de l'algorithme. En effet, si le tableau est déjà trié, l'exécution de l'algorithme de tri risque d'être très rapide comparée au cas d'un tableau totalement en désordre. C'est pour cela que l'on estime le nombre d'opérations dans le pire des cas.
En résumé, on mesure l'efficacité d'un algorithme par une expression mathématique qui indique le nombre d'opérations indispensables à l'exécution de l'algorithme en fonction de la taille des données en entrées tout en supposant le pire des cas.
Le critère de rapidité n'est pas toujours celui qui nous intéresse. On peut aussi vouloir estimer la place utilisée par un algorithme dans la mémoire de l'ordinateur. Dans ce cas, on parle de complexité spatiale alors que jusqu'à présent on considérait la complexité temporelle. La complexité spatiale peut se définir d'une manière semblable à la complexité temporelle. Dans la suite de ce cours, on s'intéressera uniquement à la complexité temporelle.
| ALGORITHME EFFICACE |
Une fois la complexité définie de manière succincte, on peut tenter de définir ce qu'est un algorithme efficace. Un algorithme sera dit efficace si sa complexité est bornée par un polynôme ayant la taille des données comme variable. Par exemple, un algorithme qui a en entrée un tableau de n éléments et qui a une complexité de n2 est un algorithme efficace. On dit aussi que l'algorithme est polynômial. Cette définition est justifiée par le fait qu'on s'intéresse aux performances des algorithmes quand la taille des données en entrée devient très importante. Par exemple, considérons les algorithmes A, B et C. Leur complexité sont les suivantes.
Ca = 80n,
Cb = 10n2,
Cc = n!.
Avec 4 éléments, il faut respectivement 320, 160 et 24 opérations aux algorithmes A, B et C pour s'exécuter. Le plus efficace pour 4 éléments est donc C. Considérons maintenant 20 éléments, il faut respectivement 1600, 4000 et 2.4 1018 opérations pour réaliser l'exécution. On s'aperçoit tout de suite que l'algorithme C n'est plus utilisable. Par contre, A et B restent applicables. Maintenant, avec 100 éléments, il faut respectivement 8000 et 100000 opérations. Bien évidemment, l'algorithme A est le plus performant, mais l'algorithme B reste applicable. Cet exemple justifie la notion d'efficacité. Si le nombre d'opérations "n'explose pas" avec une augmentation de la taille des données, l'algorithme est considéré efficace.
Certains pourraient demander ce qu'est précisément une opération. En général, on considère comme étant une opération élémentaire une affectation, une addition, un test... Mais cela est discutable puisque selon le langage et le compilateur, une opération sera exécutée plus ou moins vite, une addition s'exécutera plus ou moins vite qu'un test... Cependant, il faut bien comprendre que l'on s'intéresse au comportement général de l'algorithme face à des problèmes de grande taille. Ainsi, ce n'est pas utile de compter toutes les opérations dans le détail, ni de considérer le langage de programmation. Dans notre exemple, les coefficients 80 et 10 ne sont pas très importants, dès que la taille augmente, on s'aperçoit que c'est le terme en n qui prime. Ceci explique la difficulté à déterminer la complexité d'un algorithme. Il faut être très précis dans la démarche mais ne pas se soucier de la valeur exacte en terme de temps d'exécution de chaque opération.
| PROBLEME D'OPTIMISATION, DE RECONNAISSANCE |
| Problème d'optimisation |
Un problème d'optimisation est un problème qui consiste à chercher une meilleure solution parmi un ensemble de solutions réalisables.
| Problème de reconnaissance |
Un problème de reconnaissance est un problème qui consiste à apporter une réponse "oui" ou "non" à une question.
A chaque problème d'optimisation, on peut associer un problème de reconnaissance de la manière suivante.
Soit un problème d'optimisation:
Trouver s'S | f(s') = min{f(s) | s
S}.
Soit a un nombre, on définit le problème de reconnaissance associé:
Existe-t-il s'S | f(s')
a ?
Un problème d'optimisation est au moins aussi difficile que le problème de reconnaissance associé. De plus, on peut généralement prouver que le problème de reconnaissance n'est pas plus facile que le problème d'optimisation. En d'autres termes, cela signifie qu'un problème d'optimisation est souvent du même niveau de difficulté que le problème de reconnaissance associé. Cela justifie que la suite de ce chapitre ne concerne que les problèmes de reconnaissance.
| PROBLEME FACILE, DIFFICILE |
| Problèmes décidables |
Tout d'abord, on fait une distinction entre les problèmes décidables et les problèmes indécidables. Les problèmes indécidables sont ceux pour lesquels aucun algorithme, quel qu'il soit, n'a été trouvé pour les résoudre. Ainsi, les problèmes décidables sont ceux pour lesquels il existe au moins un algorithme pour les résoudre.
| La classe NP |
Parmi les problèmes décidables, les plus simples à résoudre sont regroupés dans la classe NP. Un problème appartient à la classe NP si quelqu'un ayant la solution au problème peut démontrer que c'est la solution en un temps polynômial. Les autres problèmes décidables sont considérés comme très difficiles. La classe NP est également décomposée en trois catégories qui permettent d'identifier les problèmes les plus simples et les problèmes les plus compliqués de la classe.
| La classe P |
La classe P, qui regroupe les problèmes les plus simples de la classe NP, contient les problèmes pour lesquels on connaît au moins un algorithme polynômial pour les résoudre. Pour le reste de la classe NP, on n'est pas sûr qu'il n'existe pas un algorithme polynômial pour résoudre chacun de ses problèmes. Ainsi, on sait que P est inclus dans NP mais on n'a pas pu prouver que P n'est pas NP.
| Réduction polynômiale |
Soit deux problèmes P1 et P2. On dit que P1 est réduit au problème P2 si on peut résoudre P1 en utilisant un algorithme pour P2 comme sous-routine. Cette réduction est dite polynômiale si l'algorithme pour P1 est polynômial en comptant l'appel à la sous-routine de P2 comme une opération élémentaire.
P2 est au moins aussi difficile que P1. En effet, si P2 appartient à la classe P, P1 y appartient aussi, car l'algorithme ci-dessus est polynômial. Si P2 n'est pas polynômial, rien n'empêche P1 de l'être s'il existe un algorithme polynômial pour le résoudre.
| La classe NP-Complet |
La classe NP-Complet regroupe les problèmes les plus difficiles de la classe NP. Elle contient les problèmes de la classe NP tels que n'importe quel problème de la classe NP leur est polynômialement réductible. Entre eux, les problèmes de la classe NP-Complet sont aussi difficiles.
| La classe NP-Difficile |
La classe NP-Difficile regroupe les problèmes (pas forcément dans la classe NP) tels que n'importe quel problème de la classe NP leur est polynômialement réductible.
| Tableau récapitulatif |
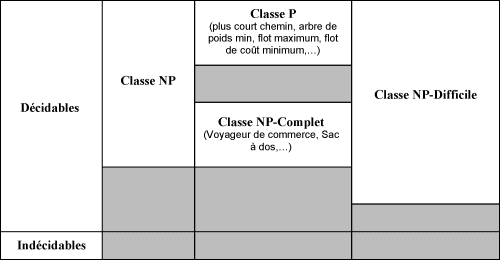
|