|
1. LES GRAPHES |
| DEFINITIONS ET THEOREMES |
| Graphe |
Un graphe est un ensemble de noeuds qui sont reliés entre eux par des arcs. Mathématiquement, un graphe est représenté par un couple de deux ensembles G = (X;U) où X est l'ensemble des noeuds et U l'ensemble des arcs.
| Arc |
Un arc relie deux noeuds entre eux, il sera donc représenté par un couple (x;y) où x et y sont des noeuds. Un arc peut être orienté, c'est-à-dire que l'ordre de x et de y est important dans le couple (x;y). Un arc peut ne pas être orienté et dans ce cas, l'ordre de x et de y dans le couple (x;y) n'a aucune importante, donc (x;y) = (y;x). Les arcs sont représentés de la manière suivante.
-
Arc orienté:

Arc non orienté:

| Remarque |
Un arc non orienté peut toujours être transformé en une situation où l'on n'a que des arcs orientés.
C'est pourquoi, dans la suite du cours, on utilisera le plus souvent des graphes orientés, c'est-à-dire des graphes dont les arcs sont tous orientés.
| Boucle |
On appelle boucle un arc dont l'extrémité initiale est égale à son extrémité finale. Par exemple, (x;x) est une boucle.
| Adjacence |
Pour un arc u = (x;y) on dit que:
x est adjacent à y,
y est adjacent à x,
x et y sont adjacents à u,
u est adjacent à x et y.
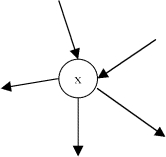
| Degré |
Le demi-degré extérieur d'un noeud est le nombre d'arcs adjacents qui en partent.
On le note d+(x) et
d+(x) = |{u ![]() U |
u = (x;y) où y
U |
u = (x;y) où y ![]() X}|.
X}|.
Le demi-degré intérieur d'un noeud est le nombre d'arcs adjacents qui y arrivent.
On le note d-(x) et
d-(x) = |{u ![]() U |
u = (y;x) où y
U |
u = (y;x) où y ![]() X}|.
X}|.
Le degré d'un noeud est le nombre d'arcs qui lui sont adjacents.
On le note d(x) et
d(x) = d+(x) + d-(x).
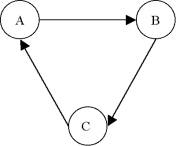
| Exemple |
Dans le graphe suivant, d+(x) = 3, d-(x) = 2, d(x) = 5.
| Graphe régulier |
Un graphe est dit régulier si les degrés de tous ses sommets sont égaux.
| Graphe complet |
Un graphe est dit complet si tous les noeuds sont adjacents deux à deux.
Autrement dit, (x;y) ![]() U
U ![]() (y;x)
(y;x) ![]() U.
U.
| Exemple |
Graphe non complet:
Graphe complet:
| Chaîne |
Une chaîne de x à y est une séquence d'arcs c = ((x;e),(z;e),(z;a)...(s;t),(u;t),(u;y)) où deux arcs qui se suivent sont adjacents et où x doit être une extrémité du premier arc et y une extrémité du dernier.
| Chemin |
Un chemin de x à y est une chaîne dans laquelle les arcs sont orientés et tels que:
x est l'extrémité initiale du premier arc,
y est l'extrémité terminale du dernier arc,
l'extrémité terminale d'un arc est l'extrémité initiale de l'arc qui le suit dans la séquence.
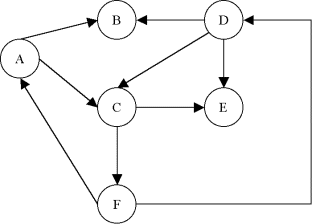
| Exemple |
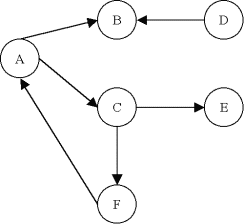
ch1 = ((A;C),(C;E)) est un chemin de A à E.
ch2 = ((A;C),(C;F),(F;A),(A;C),(C;E)) est un chemin de A à E.
ch3 = ((A;C),(C;F),(F;D),(D;C),(C;E)) est un chemin de A à E.
ch4 = ((A;B),(B;D),(D;E)) est une chaîne de A à E.
ch5 = ((A;B),(B;D),(D;C),(C;A),(A;B),(B;D),(D;E)) est une chaîne de A à E.
ch6 = ((A;B),(B;D),(D;C),(C;F),(F;D),(D;E)) est une chaîne de A à E.
| Chemin, chaîne simples |
Un chemin simple est un chemin qui ne contient pas plusieurs fois le même arc. Dans l'exemple précédent, ch1 et ch3 sont des chemins simples mais pas ch2.
Une chaîne simple est une chaîne qui ne contient pas plusieurs fois le même arc. Dans l'exemple précédent, ch4 et ch6 sont des chaînes simples mais pas ch5.
| Chemin, chaîne élémentaires |
Un chemin élémentaire est un chemin qui ne passe pas plus d'une fois par un noeud. Dans l'exemple précédent, ch1 est un chemin élémentaire mais pas ch2, ni ch3.
Une chaîne élémentaire est une chaîne qui ne passe pas plus d'une fois par un noeud. Dans l'exemple précédent, ch4 est un chemin élémentaire mais pas ch5, ni ch6.
| Connexité, forte connexité |
On définit la connexité par une relation entre deux noeuds de la manière suivante.
x et y ont une relation de connexité
il existe une chaîne entre x et y ou bien x = y.
On définit la forte connexité par une relation entre deux noeuds de la manière suivante.
x et y ont une relation de forte connexité
(il existe un chemin de x à y et un chemin de y à x) ou bien x = y.
| Graphe connexe, fortement connexe |
Un graphe est dit connexe si tous ses noeuds ont deux à deux la relation de connexité.
Un graphe est dit fortement connexe si tous ses noeuds ont deux à deux la relation de forte connexité.
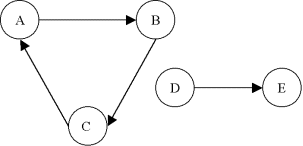
| Exemple |
Graphe non connexe:
Graphes connexes mais non fortement connexes:
Graphe fortement connexe:
| Composante connexe, fortement connexe |
On appelle composante connexe un ensemble de noeuds qui ont deux à deux la relation de connexité. De plus, tout noeud en dehors de la composante n'a pas de relation de connexité avec aucun des éléments de la composante.
De même, on appelle composante fortement connexe un ensemble de noeuds qui ont deux à deux la relation de forte connexité. De plus, tout noeud en dehors de la composante n'a pas de relation de forte connexité avec aucun des éléments de la composante.
Dans l'exemple précédent du graphe non connexe, {A,B,C} est une composante fortement connexe du graphe et {D,E} est une composante connexe.
| Graphe réduit |
On appelle graphe réduit du graphe G le graphe G' pour lequel chaque noeud est associé à une composante fortement connexe de G. De plus, un arc relie un noeud x' à un noeud y' dans le graphe G' s'il existe un arc qui relie x à y dans G où x appartient à la composante fortement connexe de G associée à x' et où y appartient à la composante fortement connexe de G associée à y'.
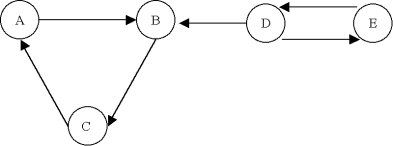
| Exemple |
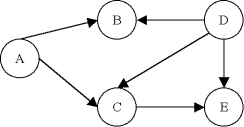
Ce graphe G n'est pas fortement connexe, car on ne peut pas trouver de chemin de A à D par exemple. Par contre, on identifie deux composantes fortement connexes A' = {A,B,C} et B' = {D,E}. Le graphe réduit du graphe G' est:
| Circuit, cycle |
Un circuit contenant un noeud x est un chemin de x à x. Un circuit est une séquence circulaire d'arcs et donc, contrairement au chemin, un circuit n'a ni début, ni fin.
De même, un cycle contenant un noeud x est une chaîne de x à x. Un cycle est également une séquence circulaire d'arcs.
Un circuit (ou une chaîne) est élémentaire si le chemin (ou la chaîne) associé(e) est élémentaire.
| Sous-graphe, graphe partiel, sous-graphe partiel |
Soit un graphe G = (X;U), X' inclus dans X et
U' inclus dans U et U'' = {(x;y) ![]() U |
x
U |
x ![]() X'
et y
X'
et y ![]() X'}.
X'}.
Le graphe (X';U'') est appelé "sous-graphe" de
G.
Le graphe (X;U') est appelé "graphe partiel" de G.
Le graphe (X';U' ![]() U'') est appelé "sous-graphe partiel" de
G.
U'') est appelé "sous-graphe partiel" de
G.
En d'autres termes:
Un sous-graphe de G, c'est G privé de quelques
noeuds et des arcs adjacents à ces noeuds.
Un graphe partiel de G, c'est G privé de quelques arcs.
Un sous-graphe partiel de G, c'est un graphe partiel d'un sous-graphe de
G.
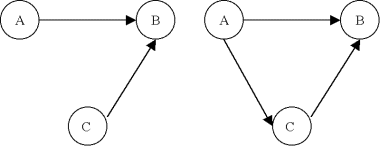
| Exemple |
Un graphe G:
Un sous-graphe de G:
Un graphe partiel de G:
Un sous-graphe partiel de G:
| COMPOSANTES FORTEMENT CONNEXES |
Lors de la conception d'un réseau de communication notamment, il peut être intéressant de savoir si la configuration choisie permet une communication de n'importe quel point à n'importe quel autre. Un moyen de le vérifier est de représenter le réseau sous la forme d'un graphe et de vérifier qu'il est fortement connexe. Pour cela, l'algorithme suivant est proposé. Il détermine la composante fortement connexe d'un graphe contenant un point donné. Ensuite, pour le problème énoncé, il suffit de choisir un point au hasard, d'exécuter l'algorithme et de vérifier que la composante fortement connexe trouvée est bien le graphe en entier. Un algorithme permettant de trouver toutes les composantes fortement connexes est également proposé.
| Recherche d'une composante fortement connexe |
Cet algorithme recherche la composante fortement connexe d'un graphe G contenant un sommet a. L'idée de cet algorithme est de parcourir le graphe à partir du point a dans le sens direct (i.e. en suivant les flèches des arcs) et de créer un ensemble des noeuds parcourus. La même chose est effectuée dans le sens indirect (i.e. en suivant les flèches des arcs en sens inverse) et de créer un deuxième ensemble des noeuds parcourus. Le premier ensemble regroupe les noeuds accessibles à partir de a et le deuxième ensemble regroupe les noeuds qui peuvent atteindre a. L'intersection de ces deux ensembles donne les noeuds qui à la fois peuvent atteindre a et sont accessibles à partir de a. Cette intersection est donc la composante fortement connexe qui contient a.
| Algorithme |
Titre: ComposanteFortementConnexe
Entrées: G = (X;U) un graphe, a un sommet.
Sortie: X' un sous-ensemble de sommets.
Variables intermédiaires: X1 et X2 deux sous-ensembles de
sommets, examiné() une fonction, x un noeud.
Début
X1 ![]() {a};
{a};
pour tout x ![]() X faire examiné(x)
X faire examiné(x) ![]() faux;
faux;
tant que ![]() x
x ![]() X1 | non examiné(x) faire
X1 | non examiné(x) faire
examiné(x) ![]() vrai;
vrai;
pour tout u = (x;y) ![]() U | y
U | y ![]() X1 faire
X1
X1 faire
X1 ![]() X1
X1 ![]() {y};
{y};
fin tant que;
X2 ![]() {a};
{a};
pour tout x ![]() X1 faire examiné(x)
X1 faire examiné(x) ![]() faux;
faux;
tant que ![]() x
x ![]() X2 | non examiné(x) faire
X2 | non examiné(x) faire
examiné(x) ![]() vrai;
vrai;
pour tout u = (y;x) ![]() U | y
U | y ![]() X2 faire
X2
X2 faire
X2 ![]() X2
X2 ![]() {y};
{y};
fin tant que;
X' ![]() X1
X1 ![]() X2;
X2;
Fin
| Recherche de toutes les composantes fortement connexes |
Pour trouver toutes les composantes fortement connexes d'un graphe, il suffit de choisir au hasard un noeud et de déterminer, grâce à l'algorithme précédent, la composante fortement connexe qui le contient. On obtient alors une première composante fortement connexe X1. Ensuite, parmi les noeuds qui ne font pas partie de X1, on en prend un au hasard pour déterminer la composante fortement connexe qui le contient. On obtient X2. On recommence ainsi jusqu'à ce que tous les noeuds appartiennent à une composante fortement connexe.
| Algorithme |
Titre: ComposantesFortementConnexes
Entrées: G = (X;U) un graphe.
Sortie: C = {C1,...,Cn} un ensemble de
composantes connexes.
Variables intermédiaires: X' un sous-ensemble de sommets, i
un entier, x un noeud.
Début
X' ![]() X;
X;
i ![]() 1;
1;
tant que X' ![]()
![]() faire
faire
choisir x dans X';
Ci ![]() ComposanteFortementConnexe(G,x);
ComposanteFortementConnexe(G,x);
X' ![]() X' - Ci;
X' - Ci;
i ![]() i + 1;
i + 1;
fin tant que;
Fin
|