|
3. REPRESENTATION DES GRAPHES |
| MATRICE D'INCIDENCE NOEUD-ARC |
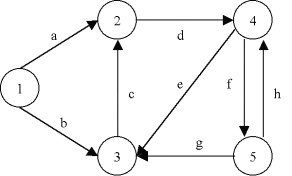
Un graphe peut être représenté par une matrice n x m (n = |X| et m = |U|), dite d'incidence, pouvant contenir uniquement les valeurs 0, 1, -1. Chaque ligne de la matrice est associée à un noeud et chaque colonne à un arc. Ainsi, une case indique la relation qu'il existe entre un noeud et un arc.
0 signifie que le noeud et l'arc ne sont pas adjacents,
1 signifie que le noeud est l'extrémité initiale de l'arc,
-1 signifie que le noeud est l'extrémité terminale de l'arc.
| Exemple |
a b c d e f g h 1 1 1 0 0 0 0 0 0 2 -1 0 -1 1 0 0 0 0 3 0 -1 1 0 -1 0 -1 0 4 0 0 0 -1 1 1 0 -1 5 0 0 0 0 0 -1 1 1
| Remarques |
Seulement 2m cases de la matrice sont non nulles sur mn cases.
Cette représentation occupe beaucoup de place en mémoire.
De plus, son utilisation apporte rarement de bons résultats au niveau des algorithmes. Notamment, pour parcourir le graphe, son emploi est difficile.
Par contre, pour quelques problèmes comme le flot de coût minimum, cette matrice a une signification directe importante et peut donc s'avérer utile.
| MATRICE D'ADJACENCE NOEUD-NOEUD |
Un graphe peut être représenté par une matrice n x n (n = |X|), dite d'adjacence, pouvant contenir uniquement les valeurs 0, 1. Chaque ligne et chaque colonne de la matrice représente un noeud. Ainsi, une case indique la relation qu'il existe entre deux noeuds.
0 signifie que les deux noeuds ne sont pas reliés par un arc,
1 signifie que les deux noeuds sont reliés par un arc orienté.
| Exemple |
Le graphe précédent sera représenté par la matrice suivante.
1 2 3 4 5 1 0 1 1 0 0 2 0 0 0 1 0 3 0 1 0 0 0 4 0 0 1 0 1 5 0 0 1 1 0
| Remarques |
Seulement m cases de la matrice sont non nulles sur n2 cases.
Cette représentation est efficace au niveau de l'espace mémoire utilisé lorsque le graphe est suffisamment dense (i.e. lorsqu'il y a suffisamment d'arcs).
Elle permet d'implémenter assez facilement les algorithmes.
Deux arcs ayant les mêmes extrémités ne peuvent pas être représentés avec cette matrice.
| LISTES |
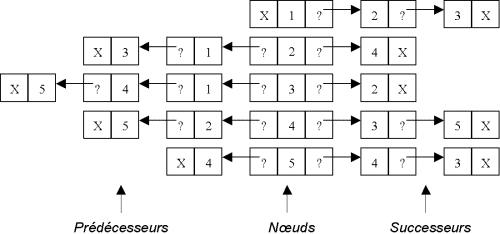
Un graphe peut être représenté par des listes. Nous proposons ici une possibilité mais de nombreuses autres peuvent convenir. On définit tout d'abord une liste des noeuds et à chaque noeud, on associe une liste de noeuds successeurs et une liste de noeuds prédécesseurs.
| Exemple |
Le graphe précédent sera représenté de la manière suivante.
| Remarques |
Cette représentation est nettement plus efficace au niveau de la mémoire occupée que les deux représentations précédentes.
Elle est très bien adaptée au parcours du graphe, aussi bien en sens direct qu'en sens indirect.
Cette structure est souple. L'ajout et la suppression d'arcs ou de noeuds sont plus aisés qu'avec les représentations matricielles.
|