|
6. ORDONNANCEMENT, RECHERCHE DU PLUS LONG CHEMIN |
| PROBLEMES D'ORDONNANCEMENT |
Les problèmes d'ordonnancement sont apparus au départ dans la planification de grands projets. Le but était de gagner du temps sur leur réalisation. De tels projets sont constitués de nombreuses étapes, également appelées tâches. Des relations temporelles existent entre ces dernières. Par exemple:
Une étape doit commencer à une date précise;
Un certain nombre de tâches doivent être terminées pour pouvoir en démarrer une autre;
Deux tâches ne peuvent être réalisées en même temps (elles utilisent une même machine par exemple);
- Chaque tâche nécessite une certaine quantité de main d'oeuvre. Il faut donc éviter, à chaque instant, de dépasser la capacité totale de main d'oeuvre disponible.
Toutes ces contraintes ne sont pas simples à prendre en compte dans la résolution du problème. Ici, nous allons nous intéresser uniquement aux deux premiers types de contraintes. On cherchera à déterminer une planification, un ordonnancement des étapes qui minimise le temps total de réalisation du projet. A partir de cette planification, nous verrons que le temps de certaines étapes peut éventuellement être modifié sans entraîner un retard du projet, alors que d'autres, les tâches dites "critiques", retardent entièrement le projet au moindre retard local.
| METHODE PERT |
Il existe deux grandes méthodes pour résoudre le problème énoncé ci-dessus. Il y a la méthode américaine CPM (Critical Path Method) avec sa variante PERT (Program Evaluation and Review Technique) et la méthode française MPM (Méthode des Potentiels). Nous nous intéresserons ici uniquement à la méthode PERT. En voici les grandes étapes.
| Représentation sous la forme d'un graphe |
Imaginons qu'un problème nous soit énoncé sous la forme suivante. Un projet est décomposé en 7 étapes (a, b ... g). La durée de chaque étape a été estimée et certaines contraintes de succession ont été établies (cf. tableau ci-après). Il s'agit maintenant de trouver la planification, i.e. les dates de démarrage de chaque étape, qui minimise le temps total de réalisation du projet, et d'indiquer dans ce cas les étapes critiques.
Durée Opérations antérieures a 1 aucune b 1 aucune c 2 b d 3 a e 2 a f 2 e g 2 d,c
La méthode PERT préconise de représenter le problème sous la forme d'un graphe. Les noeuds vont représenter des événements et les arcs des durées séparant ces événements. Tous d'abord, on définit deux sommets D et F qui représentent respectivement le début et la fin du projet. Ensuite, chaque étape est décomposée en deux événements (i.e. deux noeuds), représentant le début et la fin de l'étape, et une durée (i.e. un arc).
Etape a de durée 5:![]()
La succession de deux étapes consistera à ajouter une étape fictive de durée nulle pour indiquer que l'événement de fin de la première étape et l'événement de début de la seconde apparaissent au même instant.
a précède b:![]()
Dans ce cas précis, on peut fusionner les noeuds fa et db pour simplifier le graphe.
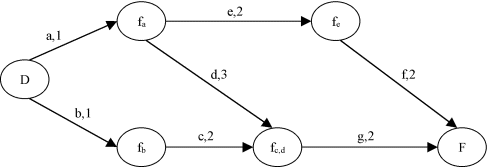
Finalement, on obtiendra le graphe suivant.
| Détermination des dates au plus tôt |
Ensuite, pour chaque événement on détermine la date à partir de laquelle il peut au plus tôt se produire. On considère la date de l'événement D comme étant 0. Ainsi, la date au plus tôt d'un événement, c'est le temps minimum qu'il faut pour que toutes les tâches antérieures soient effectuées. Toutes les tâches antérieures sont effectuées signifie qu'en suivant n'importe quel chemin en partant de D, sa longueur (i.e. la durée totale des tâches parcourues) est inférieure à la date de l'événement concerné. Autrement dit, on recherche la plus longue durée qui sépare l'événement de D. Cela revient à rechercher un plus long chemin entre D et l'événement (cf. algorithme de Bellman ci-après). Dans notre exemple, on obtient:
Finalement, on obtient pour chaque événement la date à laquelle il peut apparaître au plus tôt. Ce qui fournit la planification des tâches qui aboutit à la plus petite durée possible du projet. Maintenant, à partir de cette planification, on tente de déterminer les tâches qui ne doivent absolument pas être retardées par rapport à la planification obtenue sous peine de voir le projet entièrement retardé.
| Détermination des dates au plus tard |
De la même manière, on va tenter de déterminer la date à laquelle un événement doit au plus tard arriver pour que le projet se termine dans les temps prévus. Pour cela, connaissant la date de fin d'une étape, on est capable de déterminer la date au plus tard à laquelle l'étape doit commencer, il s'agit de la date de fin de l'étape moins sa durée. Par exemple, l'événement F doit se produire à la date 6, cela signifie que la tâche f de durée 2 doit démarrer au plus tard à la date 4 = 6 - 2. De même, quand un événement est le point de départ de plusieurs étapes, on prendra tout naturellement la date au plus tard la plus petite parmi les dates au plus tard de chaque étape. On s'aperçoit que cela revient à rechercher la durée la plus longue (i.e. le chemin le plus long) qui sépare un événement de l'événement de fin F. Cette durée est ensuite soustraite à la durée totale du projet pour fournir la date au plus tard de chaque événement. Dans notre exemple, on obtient:
| Analyse et identification des tâches critiques |
Une fois la date au plus tôt et la date au plus tard de chaque événement trouvées, on peut analyser la situation. La date au plus tôt fournie la date planifiée pour chaque événement. Ensuite, la date au plus tard indique de combien un événement peut être retardé sans retarder le projet complet. Cela identifie les étapes critiques. Il est à noter que sur le plus long chemin entre D et F, toutes les étapes sont critiques. Ici, les étapes critiques sont a, d et g. Une étape est critique si la date de début et la date de fin est critique et si la différence entre ces dates est égale à la durée de la tâche. En d'autres termes, une tâche est critique si les intervalles des dates de début et de fin sont tels qu'ils ne permettent pas une augmentation de la durée de la tâche.
| ALGORITHME DE BELLMAN |
La détermination des dates au plus tôt et des dates au plus tard est basée sur la recherche d'un plus long chemin. Comme le graphe considéré ne comporte pas de circuit, un algorithme comme celui de Bellman, plus simple que celui de Dijkstra, est très bien adapté. Il est à noter que la méthode de Bellman fonctionne aussi bien pour un plus court chemin que pour un plus long chemin, contrairement à celle de Dijkstra qui est valide uniquement pour les plus courts chemins.
L'idée de l'algorithme de Bellman pour la recherche de plus court chemin (ou de plus long chemin) est tout à fait semblable à celle de Dijkstra. La différence réside dans le choix du noeud à chaque nouvelle itération. Dans l'algorithme de Dijkstra, c'est le noeud avec la plus courte distance qui est choisi alors que dans celui de Bellman, on choisit un noeud dont tous les prédécesseurs ont déjà été traités, d'où la nécessité de ne pas avoir de circuit. Donc, sans plus de détail, voici l'algorithme de Bellman pour la recherche d'un plus court chemin.
| Algorithme |
Titre: Bellman
Entrées: R = (X;U;d) un réseau, s un
sommet.
Sorties: p() une fonction indiquant la plus courte distance qui sépare
un point de s, pred() une fonction indiquant par quel arc on arrive
à un point si on emprunte le plus court chemin.
Variables intermédiaires: S et S' deux sous-ensembles de
sommets, x et y deux noeuds, sortie un booléen,
A l'ensemble des noeuds du graphe qui n'ont pas de prédécesseurs.
Début
S ![]() {s}
{s} ![]() {A};
{A};
S' ![]() X - S;
X - S;
pour tout x ![]() X faire
X faire
p(x) ![]() +oo;
+oo;
pred(x) ![]() nil;
nil;
fin pour;
p(s) ![]() 0;
0;
sortie ![]() faux;
faux;
tant que ![]() x
x ![]() S' | tous ses prédécesseurs
S' | tous ses prédécesseurs ![]() S faire
S faire
S ![]() S
S ![]() {x};
{x};
S' ![]() S' - {x};
S' - {x};
pour chaque arc u = (y;x) | y ![]() S faire
S faire
si p(x) > p(y) + d(u) alors
[Pour le plus long chemin, remplacer par p(x) < p(y) + d(u).]
p(x) ![]() p(y)
+ d(u);
p(y)
+ d(u);
pred(x) ![]() y;
y;
fin si;
fin pour;
fin tant que;
Fin
|