|
Synchronization Problems in Hypermedia Documents |
| Bruno Bachelet Thesis Director: Philippe Mahey |
| Séminaires de l'Ecole Doctorale "Sciences pour l'Ingénieur" Clermont-Ferrand, France Presented March 9, 2000 |
| INTRODUCTION |
I am part of the LIMOS, the Computer Science, Modeling and Optimization of Systems Laboratory, Clermont-Ferrand, France. One of the specialties of the LIMOS is operations research. This area uses mathematics and computer science to bring methods implementable on computers in order to solve various theoretical and practical problems.
The LIMOS collaborates with a Brazilian research team that is working on the design and the presentation of hypermedia documents. They are confronted to problems that fit the operations research domain. In a first time, we will present some of these problems. To explain a little, a hypermedia document is mainly like an HTML document on the Internet. It is composed of different multimedia elements like sound, video, text, image... The difference here is that the content of a document is dynamic, which means we watch an animated presentation of the document.
In a second time, we will explain how, due to some simplifications, these problems can be seen as tension problems in graphs. The interest is that a graph is a way of representation for which we know numerous theoretical results. From that, we will present briefly how we adapted a method called "out-of-kilter" to solve some of those tension problems.
Finally, I will make an opening on the interest of object-oriented programming for operations research. Object-orientation is an approach for modeling that can be powerful and that is highly used in computer science at this time.
| PROBLEMS WITH HYPERMEDIA DOCUMENTS |
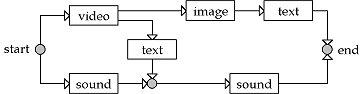
To present these problems of design and presentation of an hypermedia document, think as we were the author of such a document. We suppose we have prepared videos, sounds, images, texts... Now we must formulate the running of the presentation. The following diagram is a way to do so.
It is read this way: at the beginning of the presentation, a video and a sound are played simultaneously. When the video ends, an image and some text are displayed. Moreover, the end of the sound and the end of the text must occur at the same time. In other words, if we add the duration of the video and the duration of the text, the result must be exactly the duration of the sound. However, each object has been made previously with a fixed duration (the ideal duration). So the chance is slight for the equality to be possible. That is why during the design of an object, we add a tolerance to the planned duration.
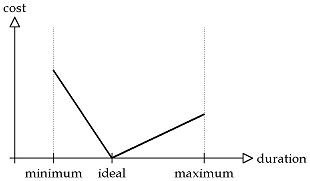
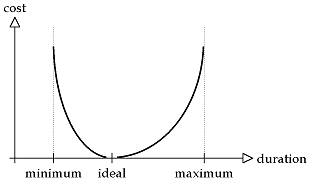
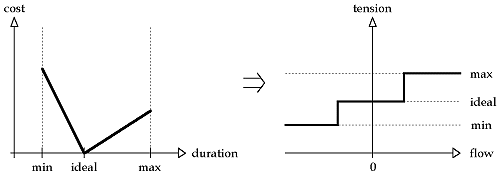
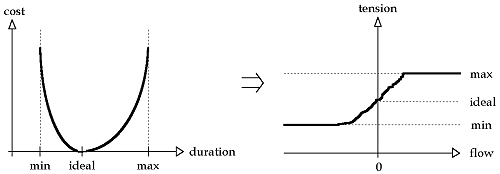
The first question we can think of is to know if the diagram built by the author is feasible. This problem can be solved quite easily. Then, we can ask ourselves what are the minimum and maximum durations of presentation of the document. Here too, answering to this question is quite simple. But the main problem, that is very hard to solve, is to schedule the duration of each multimedia element in order to fulfil the diagram constraints. All this by avoiding to be too far from the ideal durations. To solve this problem, we decide to set a cost to each object that depends on its duration. Here are two kinds of cost we are interested in. They seem to us to be representative of the real problem. The first is a piecewise linear cost, the second is a convex cost.
In both cases, we see that if an object is presented with its ideal duration, then the associated cost is null. On the other hand, the more the duration moves from its ideal value, the more the cost increases. Hence, the problem consists in scheduling the durations for the objects such as the sum of the costs is as small as possible, which we suppose to be representative of the best quality for the document. Finally, the resolution of the problem with convex costs appears to be more difficult than with linear costs.
| GRAPH AND TENSION IN A GRAPH |
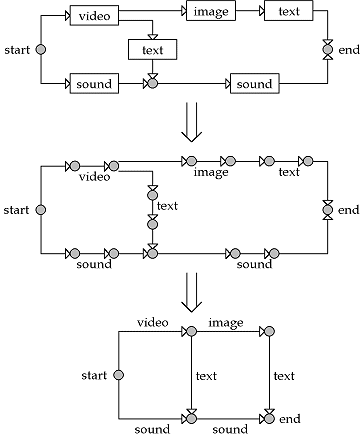
We will explain now how we can see this problem as a tension problem in a graph, knowing that we have theoretical results on graphs that will help us. We will attempt to transform the running diagram of the presentation into a graph. For that, we transform each object into two events: the start and the end of the object, symbolized by circles. These events are then separated by a duration symbolized by an arrow. We obtain then a diagram with only events and durations. Such a diagram is a graph where circles are called nodes and arrows are called arcs. We see then that some events occurred at the same time. This is the situation of the start of the presentation, the start of the video and the start of the sound. We can then reduce the graph to obtain finally a very simple representation.
In this diagram, we find again that the duration of the video plus the duration of the text is equal to the duration of the sound. That makes us think of a tension in an electrical circuit. Indeed, the durations have the same properties which are that the sum of the tensions between two points is the same using any path. Hence, our problem becomes finding a tension of minimum cost on the whole graph. We are also interested in what we call the flow of a graph. To use again the analogy with an electrical circuit, this is the current. The flow is a quantity of fluxes which goes through each arc and the sum of the fluxes incoming to a node is equal to the sum of the fluxes outgoing from it. Mathematical properties relate together the flow and the tension of a graph. These allow the method we present now.
| "OUT-OF-KILTER" METHOD |
To solve this problem of minimum cost tension, we adapted the out-of-kilter method. This method consists in defining for each arc a curve called kilter curve. The appearance of the curve depends on the kind of cost considered for the arcs. An arc will be said in-kilter if its couple (flow;tension) is on the curve. In the linear case, here is the curve.
Then we can demonstrate that if all the arcs of the graph are in-kilter, then the tension has the minimum cost. Hence our problem will be solved. The difficulty consists finally in making all the arcs in-kilter. In order to do that, we proceed by successively modifying the flow and the tension to move progressively all the arcs toward their kilter curve. In the convex case, this is a bit more complicated, because the kilter curve is continuous.
Our method can not work correctly with this kind of curve. Hence, we have to approximate it by a stepped curve, first vaguely, then the more the arcs move toward their kilter curve, the more the staircase approximation is precise, until the wanted precision.
| INTEREST OF OBJECT-ORIENTATION FOR OPERATIONS RESEARCH |
Object-orientation is an approach that allows to model lots of kinds of problem (systems, phenomena...) in a powerful and clear way. That is why it is highly used in numerous areas related to computer science, such as simulation and software engineering. Moreover, famous generic programming languages such as C++ and Java use the object-oriented technology. Then why operations research does not use this approach ?
The first reason is that the problems treated in operations research can generally be formulated in a simple way, as you could see it in this document. Hence, the power brings by an object-oriented modeling can not be used here. Moreover, a program built using object-orientation is usually slower than a program built using a classical approach. This is due to the fact that object-orientation uses relatively complex mechanisms. So, in most cases, we can say that object-orientation brings no or few fundamental evolutions in the field of operations research.
However, to estimate the efficiency of a method, we need to program it. This step is usually very long because we have to code quite complex mechanisms. With some experience, we see that for problems sometimes very different, we have to program several times things that are quite similar. Object-orientation, more than any classical approach, allows what we call reusability, which is the capacity of a software element to be reusable.
The advantages of reusability are quite obvious. Notably reusing components already written allows to develop faster new programs. Moreover, reusing a component makes it more and more reliable, because we will see more of its defaults that will be then corrected. On the other hand, it is quite obvious too that in a short time vision, object-orientation increases the development time. Indeed, we understand easily that developing reusable components takes more time than developing components that will be used only once, all this without considering that it takes time to assimilate the concepts of the object-oriented approach. These negative aspects are important to the fact that operations research uses so few of the object-oriented approach. However, in a long time vision, using object-orientation seems to facilitate the programming and the update of programs.
| CONCLUSION |
The out-of-kilter method brings satisfying results but deals with a simplified model of the problem related with the hypermedia documents. We now have to come closer to the real situations by working notably on the ways of representing the quality criteria. We will also have to consider the multimedia objects with series of discrete durations instead of tolerances around fixed values. Finally, we will have to consider random aspects related with the fact that the users of these documents can intervene on the presentation.
Concerning object-orientation, its interest seems undeniable from a practical point of view. However, how to use it is far to be obvious. If we use it too much, we will lose time writing reusable components that we will never reuse or that will excessively slow down our programs. On the other hand, not using it would deprive us of a flexibility and a rapidity of development that are not negligible.
|