|
Problèmes de synchronisation dans les documents hypermédia |
| Bruno Bachelet Directeur de thèse: Philippe Mahey |
| Séminaires de l'Ecole Doctorale "Sciences pour l'Ingénieur" Clermont-Ferrand, France Présenté le 9 mars 2000 |
| INTRODUCTION |
Je fais partie du LIMOS, le Laboratoire d'Informatique, de Modélisation et d'Optimisation des Systèmes, Clermont-Ferrand, France. Une des spécialités du LIMOS est la recherche opérationnelle. Cette discipline manipule à la fois mathématique et informatique pour apporter des méthodes implémentables sur ordinateur afin de résoudre divers problèmes théoriques et pratiques.
Le LIMOS est en collaboration avec une équipe de recherche brésilienne qui s'intéresse à la conception et à la présentation de documents hypermédia. Ils sont confrontés à des problèmes qui entrent dans le cadre de la recherche opérationnelle. Dans un premier temps, nous présenterons certains de ces problèmes. Pour donner une idée, un document hypermédia est globalement comme un document HTML sur Internet. Il est composé de différents éléments multimédia comme du son, de la vidéo, du texte, de l'image... La différence ici étant que le contenu du document est dynamique et que l'on assiste ainsi à une présentation animée du document.
Dans un deuxième temps, nous expliquerons comment, moyennant quelques simplifications, ces problèmes peuvent être vus comme des problèmes de tension dans les graphes. L'intérêt est que le graphe est un moyen de représentation pour lequel on connaît de nombreux résultats théoriques. A partir de là, nous présenterons succinctement comment nous avons adapté une méthode appelée "mise à conformité" (out-of-kilter) pour résoudre certains de ces problèmes de tension.
Finalement, je ferais une ouverture sur l'intérêt de la programmation orientée objet dans la recherche opérationnelle. Il faut savoir que l'orientation objet est une approche de modélisation qui peut être puissante et qui est abondamment utilisée en informatique à l'heure actuelle.
| PROBLEMES LIES AUX DOCUMENTS HYPERMEDIA |
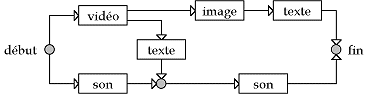
Pour présenter ces problèmes liés à la conception et à la présentation d'un document hypermédia, mettons-nous à la place de l'auteur d'un tel document. Supposons que l'on ait préparé des vidéos, des sons, des images, des textes... On doit maintenant formuler le déroulement de la présentation. Le schéma suivant peut être une manière de procéder.
Il se lit de la manière suivante: au début de la présentation, une vidéo et un son sont joués en parallèle. Quand la vidéo se termine, une image et du texte sont affichés. En outre, la fin du son et celle du texte doivent se faire en même temps. Autrement dit, si on additionne la durée de la vidéo et celle du texte, cela devrait faire exactement la durée du son. Cependant, chaque objet a été conçu à l'avance avec une durée fixe (la durée idéale). Il y a donc peu de chance pour que l'égalité soit possible. C'est pourquoi, lors de la conception d'un objet, on ajoute une tolérance à la durée prévue.
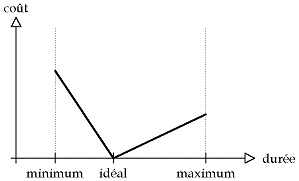
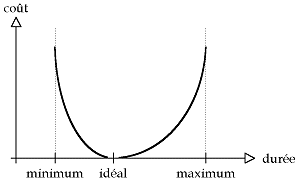
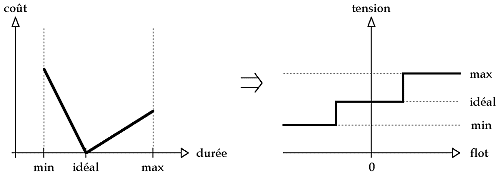
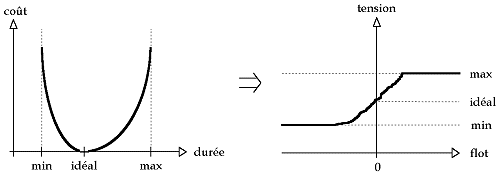
La première question que l'on peut se poser est de savoir si le schéma construit par l'auteur est réalisable. Ce problème se résout assez simplement. Ensuite, on peut se demander quelles sont les durées minimum et maximum de présentation du document. Là aussi, répondre à cette question est assez simple. Mais le problème principal, qui lui est très difficile à résoudre, reste quand même de planifier la durée de chaque élément multimédia pour satisfaire le schéma. Tout cela en évitant bien entendu de trop s'écarter des durées idéales. Pour résoudre ce problème, on décide d'imputer à chaque objet un coût, une pondération, qui est fonction de sa durée. Voici donc deux exemples de types de coût auxquels on s'intéresse. Ils nous semblent assez représentatifs du problème réel. Le premier est un coût linéaire par morceaux, le second est un coût convexe.
Dans les deux cas, on constate que si l'objet est présenté avec sa durée idéale, alors le coût associé est nul. Par contre, plus la durée s'écarte de la valeur idéale, plus le coût augmente. Le problème consiste donc à planifier des durées pour les objets de manière à ce que la somme des coûts soit la plus faible possible, ce que l'on suppose représentatif de la meilleure qualité du document. Enfin, la résolution du problème avec des coûts convexes s'avère être beaucoup plus difficile qu'avec des coûts linéaires.
| GRAPHE ET TENSION DANS UN GRAPHE |
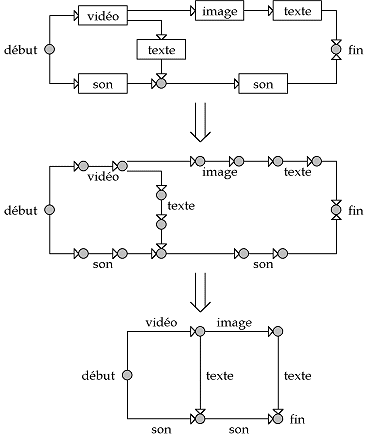
Nous allons expliquer maintenant comment on peut ramener ce problème à un problème de tension dans un graphe, sachant que l'on a des résultats théoriques sur les graphes qui vont nous aider. On va tenter de transformer le schéma du déroulement de la présentation en un graphe. Pour cela, on transforme chaque objet en deux événements: le début et la fin de l'objet, symbolisés par des cercles. Ces événements sont ensuite séparés par une durée symbolisée par une flèche. On obtient alors un schéma avec uniquement des événements et des durées. Un tel schéma est un graphe où les cercles sont appelés des noeuds et les flèches des arcs. On constate alors que certains événements se déroulent au même moment. C'est le cas notamment du début de la présentation, du début de la vidéo et du début du son. On peut donc réduire le graphe pour obtenir finalement une représentation très simple.
Sur ce schéma, on retrouve que la durée de la vidéo plus celle du texte est égale à celle du son. Cela fait penser à une tension dans un circuit électrique. En effet, les durées ont la même propriété qui est que la somme des tensions entre deux points est la même quelque soit le chemin emprunté. Notre problème revient donc à trouver une tension de coût minimum sur tout le graphe. On s'intéresse également à ce que l'on appelle le flot d'un graphe. Pour reprendre l'analogie avec un circuit électrique, il s'agit de l'intensité. Le flot est une quantité de flux qui circule dans chaque arc et la somme des flux qui arrivent à un noeud est égale à la somme des flux qui en sortent. Des propriétés mathématiques lient entre eux le flot et la tension d'un graphe. Ce sont elles qui autorisent la méthode que nous présentons maintenant.
| METHODE DE "MISE A CONFORMITE" |
Pour résoudre ce problème de tension de coût minimum, on a adapté la méthode de mise à conformité. Cette méthode consiste à définir, pour chaque arc, une courbe dite de conformité. L'allure de cette courbe dépend du type de coût considéré sur les arcs. Un arc sera dit conforme si son couple (flot;tension) est sur cette courbe. Dans le cas linéaire, voici la courbe.
On peut ensuite démontrer que si tous les arcs du graphe sont conformes, alors la tension sera de coût minimum. On aura donc résolu notre problème. La difficulté consiste finalement à rendre tous les arcs conformes. Pour cela, on procède par modification successive du flot et de la tension pour rapprocher progressivement tous les arcs de leur conformité. Dans le cas convexe, c'est un peu plus compliqué, car la courbe de conformité est continue.
Notre méthode ne peut pas fonctionner correctement sur ce type de courbe. Il faut donc l'approcher par une courbe en escalier, tout d'abord grossièrement, puis plus les arcs se rapprochent de leur conformité, plus on affinera l'approximation en escalier, jusqu'à la précision voulue.
| INTERET DE L'ORIENTE OBJET DANS LA RECHERCHE OPERATIONNELLE |
L'orienté objet est une approche qui permet de modéliser toutes sortes de problème (systèmes, phénomènes...) d'une manière très puissante et claire. C'est pourquoi elle est abondamment utilisée dans de nombreux domaines liés à l'informatique, comme notamment la simulation et le génie logiciel. En outre, des langages de programmation génériques très répandus comme C++ et Java utilisent la technologie orientée objet. Alors pourquoi la recherche opérationnelle n'utilise-t-elle pas cette approche ?
La première raison est que les problèmes traités en recherche opérationnelle peuvent généralement être formulés de manière simple, comme vous avez pu le constater dans ce document. Ainsi, la puissance apportée par une modélisation orientée objet ne peut pas être exploitée ici. De plus, un programme conçu en orienté objet est généralement plus lent qu'un programme conçu avec une approche classique. Ceci est dû au fait que l'orienté objet met en oeuvre des mécanismes relativement complexes. Donc, d'une manière générale, on peut dire que l'orienté objet n'apporte pas ou peu d'évolutions fondamentales dans la recherche opérationnelle.
Cependant, pour juger de l'efficacité d'une méthode, il faut la programmer. Cette phase est généralement assez longue par le fait que l'on doit coder des mécanismes assez compliqués. Avec l'expérience, on s'aperçoit également que pour des problèmes parfois très différents, on est amené à reprogrammer des choses assez similaires. Et bien l'orienté objet, beaucoup plus qu'une approche classique, permet ce que l'on appelle la réutilisabilité qui est la capacité d'un élément logiciel à être réutilisable.
Les intérêts de la réutilisabilité sont assez évidents. Notamment le fait de réutiliser des composants déjà écrits permet de développer plus rapidement de nouveaux programmes. En plus, le fait de réutiliser un composant le rend de plus en plus fiable, car on s'apercevra beaucoup plus de ses défauts qui pourront ensuite être corrigés. Par contre, il est assez évident aussi qu'à court terme, l'orienté objet rallonge les temps de développement. En effet, on comprend facilement que développer des composants réutilisables est plus long que de développer des composants utilisés qu'une seule fois, ceci sans compter qu'il faut du temps pour assimiler les concepts de l'approche orientée objet. Ces aspects négatifs contribuent énormément au fait que la recherche opérationnelle n'utilise que peu la programmation orientée objet. Cependant, à long terme, utiliser l'orienté objet semble tout de même faciliter la programmation et la mise à jour des programmes.
| CONCLUSION |
La méthode de mise à conformité apporte des résultats assez satisfaisants mais porte sur un modèle simplifié du problème lié aux documents hypermédia. Il faut donc maintenant que l'on se rapproche des situations réelles en travaillant notamment sur d'autres manières de représenter les critères de qualité. Il faudra également que l'on considère les objets multimédia avec des possibilités de durées discrètes au lieu de tolérances autour de valeurs fixes. Enfin, il faudra aussi prendre en compte des aspects aléatoires liés au fait que les utilisateurs de ces documents peuvent intervenir sur la présentation.
En ce qui concerne l'orienté objet, son intérêt semble indéniable d'un point de vue pratique. Cependant son utilisation est loin d'être évidente. Si on en abuse, on va perdre du temps à écrire des composants réutilisables que l'on ne réutilisera jamais ou qui ralentiront excessivement nos programmes. D'un autre côté, ne pas l'utiliser nous priverait d'une souplesse et d'une rapidité de développement non négligeables.
|