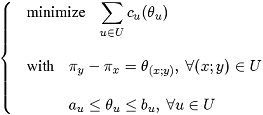|
Aggregation Method for Tension Problems |
| Bruno Bachelet (LIMOS, Clermont-Ferrand, France) |
| 4th Francoro International Conference Fribourg, Switzerland August 17-21, 2004 |
The study of tension problems in graphs is motivated here by synchronization problems in hypermedia documents (cf. [2]). They are composed of various media objects such as sound, video, text, image, applet... Authors need powerful tools to schedule automatically the temporal specifications of these objects in a document. Any media object u has an intrinsic duration, also called ideal, ou and an interval [au;bu] in which its effective (i.e. scheduled) duration can vary. The author also specifies temporal constraints in order to express the way the presentation of the document should happen. The problem is finally to schedule the duration of each media object so it satisfies both the tolerance intervals and the temporal constraints.
This problem can be interpreted as a minimum cost tension problem in a graph. Let
![]() be a function that assigns a potential to each node of a graph
G = (X;U). The tension
be a function that assigns a potential to each node of a graph
G = (X;U). The tension
![]() of an arc u = (x;y) is the difference of potentials
of an arc u = (x;y) is the difference of potentials
![]() and is constrained to
and is constrained to
![]() . The minimum cost tension problem can be modeled as:
. The minimum cost tension problem can be modeled as:
To measure the quality of a document, many proposals were made. The first studies consider piecewise linear costs, with a minimum for ou (e.g. [4]). The problem can thus be expressed as a linear program and many polynomial algorithms were developed (e.g. [1]). Recently, we proposed an aggregation method (cf. [3]) to solve the minimum convex piecewise linear cost tension problem (or CPLCT problem) on series-parallel graphs (or SP-graphs). It was shown to be competitive on this class of graphs with the best algorithms.
However, the number of objects that need to be modified (i.e. that are not scheduled at their ideal duration) is also relevant for hypermedia synchronization. Altering the duration of a media object is CPU consuming, thus in a real time context, minimizing this operation is important (cf. [5]). We propose here an aggregation approach for the minimum binary cost tension problem (or BCT problem) in a SP-graph, where the cost functions are defined as:
Due to its discrete nature, this problem is NP-complete, on graphs with non-specific structure as well as series-parallel graphs (cf. [5]).
Our interest in SP-graphs is explained by the structure of the temporal constraints in hypermedia synchronization that is very close to series-parallel. Nevertheless, SP-graphs represent situations that are too ideal. The notion of quasi-k SP-graphs is thus introduced to regroup the graphs whose series-parallel property is somewhat altered (disturbing arcs are added). Therefore, those graphs represent perfectly the needs to express the synchronization of media objects.
To sum up, we introduce SP-graphs and the general aggregation method, and we present briefly its application to the CPLCT problem on SP-graphs, before extending and combining it with the out-of-kilter approach to solve the problem on quasi-k SP-graphs. For this last approach, called reconstruction, the problem of decomposing any graph into series-parallel components is discussed. We also propose an application of the aggregation method to the BCT problem. Finally, we conclude with a comparative study, both theoretical and practical, of these methods and some others that already exist.
| [1] | Ravindra K. Ahuja, Dorit S. Hochbaum and James B. Orlin, "Solving the Convex Cost Integer Dual Network Flow Problem", Management Science 49, 2003, 950-964. | |
| [2] | Bruno Bachelet, "Modélisation et optimisation de problèmes de synchronisation dans les documents hypermédia", PhD Thesis, Université Blaise Pascal, Clermont-Ferrand, France, 2003. | |
| [3] | Bruno Bachelet and Philippe Mahey, "Minimum Convex-Cost Tension Problems on Series-Parallel Graphs", RAIRO Operations Research 37-4, 2004, 221-234. | |
| [4] | M. Cecelia Buchanan and Polle T. Zellweger, "Specifying Temporal Behavior in Hypermedia Documents", European Conference on Hypertext '92, 1992, 262-271. | |
| [5] | Celso C. Ribeiro and Eric Sanlaville, "On the Complexity of Scheduling with Elastic Times", Research Report, Computer Science Department, PUC-Rio, Rio de Janeiro, Brazil, 2002. |